That ratings nightmare again

[Dave242]

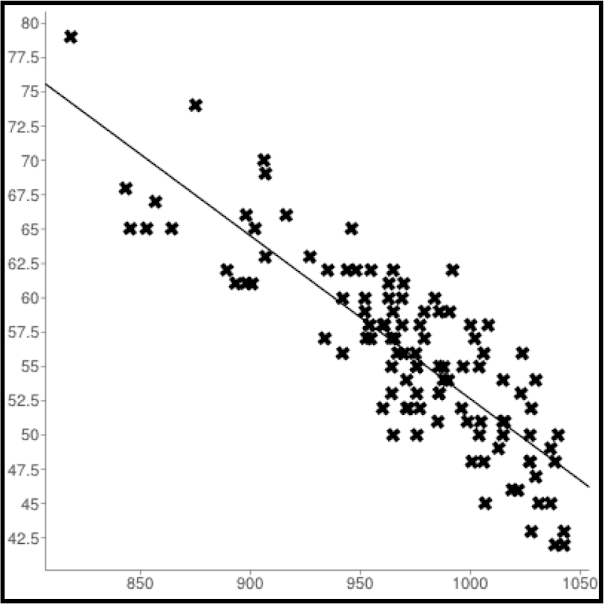
Its not very accurate, but it works for now. Just gotta live with it until something better comes along.

It is actually very accurate and stable.

The variations in SSA that I have observed almost never are more than +/- 1 throw (barring crazy weather or lack of enough propagators to make things statistically valid).

It makes no sense to worry about accuracy of less than +/- 1.49 throws, since that gets rounded to 1 throw.....and there is no way that I know of to throw a disc in less than 1 throw (or a non-integer number of throws).

edit: BTW, this is why I am asking to see the event stats. I want to see examples of variations greater than +/- 1.49.

 

[jeverett]

As an example, the starting ratings ranking of Open players at Worlds has had a 91-95% correlation to their finishing rank. I'd say that's pretty predictive.

I agree, correlation in that range is *great*, however the white paper on the topic also had event examples with correlations considerably lower (sometimes even below 50%). I was also curious as to why the statistics only included the MPO correlation, and not the correlation for other divisions or overall. I would think that ideally, the correlation calculations should be run on (at least) all propagators for an event, and not limited to a specific division.

For reference, if anyone wants to see that white paper, it is available here:

http://www.pdga.com/files/documents/Correlation_for_Better_Courses.pdf

 

[jeverett]

I'll profess to ignorance; I haven't been involved in other sports or competitions that used such ratings. My background is in team sports.

I would imagine you could take the PDGA ratings and have some kind of predictive factor. A player with a 900 rating will shoot 50 points over or under his rating xx% of the time. Or, a player with a 900 rating will beat a player with a 930 rating on a particular SSA course xx% of the time in a given round, and xx% of the time over 4 rounds. Something like that.

Just as it can be converted to handicaps, if desired.

You can definitely do this, however the rating system itself wasn't built around enforcing consistency of that kind of relationship. By comparison to most other rating systems, there are two things the PDGA rating system doesn't really do: 1. in most rating systems, players who have never played before still have a rating, and there is a fixed (win/loss ratio) relationship between the lowest and highest possible ratings (and every possible point in between them) in the scale, and 2. most rating systems actually use two measurements, the visible 'rating' and an internal measure of just how accurate (subject to fluctuation) that rating is.

For example, a player with only a few matches has a rating, that externally may look the same as another player who's been competing for years.. but internally the new player has a measurement that indicates their rating is very 'provisional' (i.e. less valuable as a benchmark), and will be weighted very lightly when it comes to applying the results of their matches on subsequent ratings. As the player plays more and more matches, this internal value gets smaller (i.e. their rating becomes a better and better benchmark of how a player of that rating performs).

By comparison, in the PDGA system a player goes from having no rating at all to having a rating of how they did at their first match. Once they've become a propagator, every round they play is considered equally-as-important as every round of every other propagator, regardless of the total number of matches for each individual.

 

[Cgkdisc]

I agree, correlation in that range is *great*, however the white paper on the topic also had event examples with correlations considerably lower (sometimes even below 50%). I was also curious as to why the statistics only included the MPO correlation, and not the correlation for other divisions or overall. I would think that ideally, the correlation calculations should be run on (at least) all propagators for an event, and not limited to a specific division.

For reference, if anyone wants to see that white paper, it is available here:

http://www.pdga.com/files/documents/Correlation_for_Better_Courses.pdf

The correlations were done with MPO simply due to larger field sizes. Note that the 91-95% correlation is for the whole event other than the Final 9 which includes at least 7-8 rounds. The white paper primarily looked at 2 rounds on the same course where the correlations were lower.

 

[jeverett]

The correlations were done with MPO simply due to larger field sizes. Note that the 91-95% correlation is for the whole event other than the Final 9 which includes at least 7-8 rounds. The white paper primarily looked at 2 rounds on the same course where the correlations were lower.

I think this is another interesting example.. we're really looking at per-event correlations rather than per-round ones, and because (official) SSA's and round ratings are often computed using all event rounds, this makes sense. But it also means that we're getting much more meaningful data (i.e. higher correlations) out of many-round events, yet we treat ratings produced in 2-round events as just as important/predictive as ratings produced in many-round events (i.e. getting back to the fact we're missing an internal value measuring just how accurate any given rating is).

As an example, in competitive Backgammon (yes, there is indeed competitive Backgammon), because the number of total matches played per 'game' is variable, the number of matches per game is applied to their internal rating accuracy measurement (i.e. the more matches in the game, the more significant the rating produced by that game is on subsequent player ratings).

 

[krupicka]

The same is done for the PDGA ratings substituting number of holes in a round for matches in a game.

 

[jeverett]

The same is done for the PDGA ratings substituting number of holes in a round for matches in a game.

Hi Krupicka,

Hmm.. we must be talking about different things. For example, compare the relative weights of four 1-round events with one 4-round event. In the PDGA system, while the four rounds of the 4-round event will probably be averaged for purposes of the SSA and ratings calculations, the effect on player ratings of the four single rounds and the four-round event will be the same (they have the same weight), despite the fact we *know* that the 4-round event will have a higher overall correlation between player rating and event score.

In the Backgammon system, the 4-round event would have a vastly more significant impact on the overall rating of the players than four 1-round events would.

 

[Cgkdisc]

Interestingly, we looked at whether players (super props) who had a standard deviation below a certain threshold would produce better numbers than using all props. It turned out that having more total props of all standard deviations was more important (better) than using a smaller number of super props with a tighter range of scoring.

 

[jeverett]

Interestingly, we looked at whether players (super props) who had a standard deviation below a certain threshold would produce better numbers than using all props. It turned out that having more total props of all standard deviations was more important (better) than using a smaller number of super props with a tighter range of scoring.

Hmm.. I wonder, though, if that doesn't have something to do with the problems with assuming a linear relationship between player rating and round/event score. When you take the 'super prop' group, the linear regression produced by this small group is not necessarily representative of the linear regression produced by the larger group. For example, take a look at a quick plot of a round of the Memorial:

If you just grab the group rated 1020 and above there, you definitely don't get a linear regression remotely close to what you get if you run it on the whole field.

Edit: i.e. a small group of higher-rating-accuracy players is not necessarily better than a larger group of moderately-accurate-rating players.

As an aside, have attempts been made to find a better algorithm than linear to approximate the relationship between player rating and round/event score across all events?

 

[Cgkdisc]

Remember that higher rating doesn't mean they are a Super prop. A Super prop would be players with lower personal standard deviations which occurs at all rating levels with a slight bias toward higher rating.

There's no reason to believe the relationship is anything but linear in terms of measurability. All shots have a different difficulty level but we don't have a way to assess a more precise value than "one throw." If we had a way to assign decimal values to throws where maybe a really good throw counted 0.7, an average throw 1.0 and a weak throw 1.3 (including decimal values between these values) we might discover any non-linearities that may be in there.

 

[jeverett]

There's no reason to believe the relationship is anything but linear in terms of measurability. All shots have a different difficulty level but we don't have a way to assess a more precise value than "one throw." If we had a way to assign decimal values to throws where maybe a really good throw counted 0.7, an average throw 1.0 and a weak throw 1.3 (including decimal values between these values) we might discover any non-linearities that may be in there.

There are lots of events where I'd agree that the results come out very nicely linear, but occasionally I also come across events (like the Memorial) where across every round (for example) the group above 1020 is not distributed in the same kinds of patterns as the rest of the field. Definitely, given the stepwise nature of round/event scores, coming up with something (accurate) other than linear is going to be a challenge.

I do wonder, though, if it might not be possible to assess the mathematical relationships between shot "difficulty levels" and player ratings. For example, what is the mathematical relationship between player rating and (of course averaged) putting accuracy as distance increases? Or what is the mathematical relationship between player rating and averaged drive length + averaged putt distance? I definitely don't have the data to answer any of those.. but it does make me wonder if a better non-linear fit line couldn't still be engineered, even with the stepwise problem.

 

[Steve West]

Hmm.. I wonder, though, if that doesn't have something to do with the problems with assuming a linear relationship between player rating and round/event score.

No, it's because with backgammon (or chess or match play) each player is measured against only one other player. In those cases, the accuracy of the information about the opponent does make a difference. An error in measuring the skill of THE opponent is not cancelled out, so it is wise not to trust it completely.

With PDGA ratings, everyone is playing against ALL the other players. In that case, the more information that goes in, the better. Any error of measuring the skill of any single player will be washed out.

 

[jeverett]

No, it's because with backgammon (or chess or match play) each player is measured against only one other player. In those cases, the accuracy of the information about the opponent does make a difference. An error in measuring the skill of THE opponent is not cancelled out, so it is wise not to trust it completely.

With PDGA ratings, everyone is playing against ALL the other players. In that case, the more information that goes in, the better. Any error of measuring the skill of any single player will be washed out.

That's a good point, and a definite advantage to large-group 'sports' like disc golf, as opposed to 1v1 games and activities. Plus, we're able to measure "by how much" did player x score 'better' than player y, something that is really difficult (or impossible) to be accurate about with many other games.

 

[jeverett]

With PDGA ratings, everyone is playing against ALL the other players. In that case, the more information that goes in, the better. Any error of measuring the skill of any single player will be washed out.

Thinking more about this, though, what does that say about the PDGA system of 'propagators'? We're only using players with at least 8 previous rounds for ratings calculations, so clearly there must be *some* level of inaccuracy/error which can't be 'washed out' (without a sample size much larger than was present at the event). Or as sample size decreases, at what point does error of measuring skill exceed the value/weight of that player's rating?

 

[Steve West]

Thinking more about this, though, what does that say about the PDGA system of 'propagators'? We're only using players with at least 8 previous rounds for ratings calculations, so clearly there must be *some* level of inaccuracy/error which can't be 'washed out' (without a sample size much larger than was present at the event). Or as sample size decreases, at what point does error of measuring skill exceed the value/weight of that player's rating?

If every player stayed at a fixed skill level, or even if each player fluctuated around a skill level, it would all tend to wash out. Especially as more and more rounds go into a particular player's rating.

I think the 8 rounds minimum has more to do with avoiding the steep part of the learning curve. But I don't know.

 

[Cgkdisc]

The eight rounds came from the origin of the system when 8 rounds at the 1998 Cincy Worlds produced the first roughly 300 propagators. It's interesting that since then, the average PDGA member plays about 16 rated rounds per year. That would mean that a player at that participation level would have enough rounds to be a propagator in about 6 months. Not sure if we were just lucky but it seems like the system is working with props starting at 8 rounds. Also, the most recent rounds are double weighted which makes the rating just a bit more connected to current performance.

 

[krupicka]

Hi Krupicka,

Hmm.. we must be talking about different things. For example, compare the relative weights of four 1-round events with one 4-round event. In the PDGA system, while the four rounds of the 4-round event will probably be averaged for purposes of the SSA and ratings calculations, the effect on player ratings of the four single rounds and the four-round event will be the same (they have the same weight), despite the fact we *know* that the 4-round event will have a higher overall correlation between player rating and event score.

In the Backgammon system, the 4-round event would have a vastly more significant impact on the overall rating of the players than four 1-round events would.

What I was referring to is that a 27 hole round is weighted more heavily than an 18 hole round when computing a players rating.

 

[jeverett]

What I was referring to is that a 27 hole round is weighted more heavily than an 18 hole round when computing a players rating.

I actually (just recently) checked on that, and they appear to scale the same. For example, if the 18-hole course has an SSA of 54, and the 27-hole course has an SSA of 81, the rating increment for the 27-hole course will be precisely 2/3 (actually the ratio of 18 / number_of_holes) that of the rating increment for the 18-hole course. e.g. if the rating-per-throw-interval for the 18-hole round came out at 9, on the 27-hole round it would come out at 6. That way, being two under SSA after 18 on the first layout (1000 + 2 * 9 = 1018) will rate exactly the same as being three under SSA after 27 (1000 + 3 * 6 = 1018). This can be verified by looking at mixed 18- and 27-hole events. Does that help?

 

[araytx]

I have a problem that I believe a few might have. I played in a tournament recently which featured two courses. I played intermediate and got a rating for my round. The advanced and open players played the same course later on that day and got higher ratings. Fair enough conditions were a bit different.

A year ago I had the same situation however the conditions I faced were tougher than the advanced players and got lower ratings for the same course, same tees. What gives? Is anyone ever going to come up with a fair ratings system for this sport.

Granted some of you will say your rating should not matter but it does if you know you are a way better player than the rating suggests and you are a rec rated player yet you play like an intermediate borderline advanced player.

Side note the pdga app seems to do a better job in ratings than that confusing propagator system maybe that would be the way to go. It might alleviate the large number of players that are in the intermediate ranking that really should be advanced rated players.

Beezy, if you're talking about Lewisville, there is something that should be different at official ratings. There's no way your 54 at Lake Park in the morning round should be 40 points different than a 54 that afternoon in our rounds.

They may not be exactly even, but there should be some change.

 

[mashnut]

I actually (just recently) checked on that, and they appear to scale the same. For example, if the 18-hole course has an SSA of 54, and the 27-hole course has an SSA of 81, the rating increment for the 27-hole course will be precisely 2/3 (actually the ratio of 18 / number_of_holes) that of the rating increment for the 18-hole course. e.g. if the rating-per-throw-interval for the 18-hole round came out at 9, on the 27-hole round it would come out at 6. That way, being two under SSA after 18 on the first layout (1000 + 2 * 9 = 1018) will rate exactly the same as being three under SSA after 27 (1000 + 3 * 6 = 1018). This can be verified by looking at mixed 18- and 27-hole events. Does that help?

I don't think that's what Krupicka was talking about. He was saying that a 27 hole round affects your rating 1.5 as much as an 18 hole round (e.g. if your rating was based on 2 rounds, 1 18 hole and 1 27 hole then the rating would be weighted .6 to the 27 hole round and .4 to the 18 hole round rather than them equally factoring in to the overall rating).