Disc Physics

[jubuttib]

I think you underestimate the way directional energy is diverted as the disc fades - the disc doesn't stop

Never said it would, actually I suspect it'd speed up while fading, leading to the air speed increasing so much that it'd stop fading (having reached cruising speed again). What I thought about at first was that it could perhaps pull out of the dive if it sped up enough during the descent, due to the inevitable turn resulting from the high speed. According to JHern though the turn would serve only to increase the nose down, making it dive even faster, which actually makes sense since we've known for quite a while that hyzerflipping a disc often leads to more nose down.

It's entirely logical that a disc can maintain air speed because mainly through gravity, while the fade keeps it turning towards the left - if it has enough room to descent, it will describe a full helix.

If it has enough room, sure. A slope like that doesn't seem like enough space by any means.

In the video, the disc descends much faster than it moves horisontally in this phase, so it looks as if it drops a bit, then moves a bit towards the right before it hits.
I think

I assume you're talking about the way the flight path looks in the camera?

 

[JR]

Unfortunately i haven't been able to find a way with which to make equal height vertical yardsticks have the tops at equal height from the ground.

Garden designers use clear, flexible tubing filled with water. The water line gives you a perfect level. Don't try this in Finland during winter (well, maybe with antifreeze).

I'm not sure of how exact to level the sticks need to be for aerodynamic coefficient calculations. I don't see how i could be accurate in gauging the water level any better than approximating by sight. I assume you mean that the vertical yard sticks for height that JHern needs for the measurements have that clear tube half filled with water on top of the yard sticks. It would require more work because the yardsticks would need to be able to stand up with the sticks one meter apart. Unfortunately a level top ain't enough. With luck i might avoid soccer players and school PE classes at a soccer field but until such a system is used on the field i can't tell if it's even. It had trouble after a change artificial turf. It' developed air bubbles at parts between the turf and the ice on top of it. So the ice cracked. It's used for skating during winters. Since the ground and tops of the yardsticks need to be level and the yardsticks perfectly upright and equal length for the measurements JHern needs, it's a chore to manufacture those sticks and stands for them. That is why it would be a good idea to get a piece of clear tube and measure the field first. If that works then it might be more realistic to try to make the yard sticks and film enough throws to possibly give JHern enough data to perform analysis. It will take months before the snows will have melted. I can't make any promises because of filming duties. I spent around 20 hours this week on pre production work of one competition from 2010. While making arrangements for filming abroad this year.

 

[Moseley]

If it has enough room, sure. A slope like that doesn't seem like enough space by any means.

In the video, the disc descends much faster than it moves horisontally in this phase, so it looks as if it drops a bit, then moves a bit towards the right before it hits.
I think

I assume you're talking about the way the flight path looks in the camera?

Yeah, all in reference to the POV. Remember that it's all distorted by a zoom lens as well as perspective, the landing site is actually waaay down and not that steep.

 

[jubuttib]

Which further enhances my view. If you don't want the mountain to get in the way of the full helix, the slope would either have to be really damn steep or the discs spiral really damn tight. Damn tight spiral would necessitate a damn big hyzer angle, necessitating a damn fast dive towards the ground. That, or weird winds.

 

[Monocacy]

Unfortunately i haven't been able to find a way with which to make equal height vertical yardsticks have the tops at equal height from the ground.

Garden designers use clear, flexible tubing filled with water. The water line gives you a perfect level. Don't try this in Finland during winter (well, maybe with antifreeze).

I'm not sure of how exact to level the sticks need to be for aerodynamic coefficient calculations. I don't see how i could be accurate in gauging the water level any better than approximating by sight. I assume you mean that the vertical yard sticks for height that JHern needs for the measurements have that clear tube half filled with water on top of the yard sticks.

No, I explained poorly. You would run a long piece of clear, flexible tubing between two of your yardsticks (meter sticks?). Fill the flexible tubing with water, and the water level at one end of the tubing will be exactly the same as the water level at the other end of the tubing. Mark the level spot, and move on to your next yard / meter stick.

In case I have explained poorly again, here are some links that provide more detail on making and using a water level:

http://factsfacts.com/MyHomeRepair/WaterLevel.htm

http://www.suite101.com/content/how-to-make-and-use-a-water-level-a87767

 

[JR]

I got you. The problem is that i don't know if my eyes are good enough for measurement accuracy that JHern needs so how about it JHern? I was thinking that a longer tube would be more accurate. Preferably from end to end but that may prove to be more difficult. Assuming half filling the tube looking at it trying to match the tube water level at the ends at exactly half height of teh tube's inner diameter is the most accurate way to do this. Unfortunately JHern needed quite a long measurement distance so the construction would get even more challenging and probably expensive.

 

[DagG]

Rather than compensating for a surface which is not level, why not use one that already is? Are there any frozen lakes in your parts?

 

[JR]

The official snow depth is at 54 cm that kind of complicates things. I don't think i'm gonna shovel that much snow with the footing being what it is because that will change the way the discs fly because the throw is more back to front running than rotating on top of back to front motion. And that is a flaw in my form anyway until my ankle can reliably take heel pivots without a brace. I kicked a runway free then after snow fall relatively free of snow. Oh boy... No joy. Even ice ain't necessarily flat unfortunately. The surface can be uneven. Especially in the sea by which i live. Which is another problem. I've watched the pages of Finnish Meteorological Institute almost each day this winter for throwable weather and i've never ever seen a stop to the winds. This test needs to be performed on a calm moment.

 

[Muddyboots]

Wades back in to discussion...... So I have a relatively simple question. This pertains to the throwing downhill theory. It would seem to me that for obvious reasons, thowing off the top of a mountain would give you the opportunity for the absolute longest throw ever. Would I be correct in assuming (purely theoretical and unachievable) that if you threw a disc off the top of a slope, no wind, and managed to get the disc to cruising speed (equilibrium) where the disc plane was paralell to the ground (i.e. flat as viewed from the thrower) that the limiting factor in terms of distance/duration would be the fact that the disc would eventually stop spinning? Certainly it would have to be the perfect shot so that acceleration due to gravity didn't cause the disc to turn, or speed loss resulting in fade. Pure theory here. How steep would the slope have to be? Does gravity not influence the rotational momentum of an object at all? Trying to wrap my head around this.
KP

 

[Monocacy]

I got you. The problem is that i don't know if my eyes are good enough for measurement accuracy that JHern needs so how about it JHern?

Measurement is as accurate as reading a meniscus, which can be pretty accurate. Online engineering supply stores do sell ends with calibrated markings, but accuracy still depends on reading a meniscus so I'm not sure it would be worth spending the money.

I was thinking that a longer tube would be more accurate. Preferably from end to end but that may prove to be more difficult. Assuming half filling the tube looking at it trying to match the tube water level at the ends at exactly half height of teh tube's inner diameter is the most accurate way to do this. Unfortunately JHern needed quite a long measurement distance so the construction would get even more challenging and probably expensive.

I did a quick online search, and lab-grade Tygon tubing is available for about $1 USD per foot. That should give a ballpark idea of cost. How far apart did you plan to space the markers?

 

[JR]

In Finland tubing is probably expensive. I was thinking of follow the guidelines from JHern because he needs the data. The details are in an earlier page of this thread and the tubing would have to be long. I would imagine that with a long tube the accuracy would be god enough. Getting a level surface and making the meter sticks and getting each of them upright under the tube is gonna be a mess. And expensive and time consuming to build and set up. In cold weather the water in the tube would freeze so that's not easy to use.

NMTC: Dave Dunipace wrote on the PDGA forum that a disc stops spinning about between 20 and 25 seconds. The disc can still fly forward after complete stopping of the spin. If the HSS is good enough and the disc is aligned correctly relative to the flight path. And there's no wind to tilt the disc off of the direction of the flight. As to degrees of slope it's way beyond my knowledge at this point to calculate that for any given discs. And not many probably have proper data of the performance of any disc for that kind of calculations. The more height there is between the equilibrium flight path of the disc and the ground and the steeper and faster the disc is flying at when the spin stops the farther the momentum has the possibility of carrying the disc. It's another matter to which direction it will go.

I think the nose angle and the angle of attack(nose angle relative to the flight path) do influence the rotational momentum vs gravity. At least in that if you change the nose angle and angle of attack or keep them the same and adjust the steepness of the dive the vector of the gravity is gonna be different. Aerodynamic precession is something that needs to be looked at in conjunction with the previous things. Somebody else had better explain that.

Last winter i tried to putt with minimal arm motion and filmed myself obliquely from above and behind toward my practice basket. It is difficult to minimize spin. At best i got about a fifth of a rotation on putters flying for about 7' without wobble. Not only was it difficult to reduce the spin rate that much but it was even more difficult to do it simultaneously with a wobble free flight. My success rate was low with so low spin rates. I was able to increase spin rate without wobble to much higher success rates. I didn't write down or memorize exact numbers but the magnitude was almost one offs to IIRC one half rotation of the putter in that 7' of flight without wobble for like 50-66% range of attempts. With slight wobble the success rate went way up with half a revolution of spin to 7'. Had i trained more for one specific version of putting the success rate of both spin rates would have likely gone up. Neither way is or has ever been my normal putting motion. So the success rates should be higher for those using one or the other of the kinds of putts all the time. I had virtually no practice for either kind of putting motion then.

 

[Muddyboots]

NMTC: Dave Dunipace wrote on the PDGA forum that a disc stops spinning about between 20 and 25 seconds. The disc can still fly forward after complete stopping of the spin. If the HSS is good enough and the disc is aligned correctly relative to the flight path. And there's no wind to tilt the disc off of the direction of the flight. As to degrees of slope it's way beyond my knowledge at this point to calculate that for any given discs. And not many probably have proper data of the performance of any disc for that kind of calculations. The more height there is between the equilibrium flight path of the disc and the ground and the steeper and faster the disc is flying at when the spin stops the farther the momentum has the possibility of carrying the disc. It's another matter to which direction it will go.

I think the nose angle and the angle of attack(nose angle relative to the flight path) do influence the rotational momentum vs gravity. At least in that if you change the nose angle and angle of attack or keep them the same and adjust the steepness of the dive the vector of the gravity is gonna be different. Aerodynamic precession is something that needs to be looked at in conjunction with the previous things. Somebody else had better explain that.

Last winter i tried to putt with minimal arm motion and filmed myself obliquely from above and behind toward my practice basket. It is difficult to minimize spin. At best i got about a fifth of a rotation on putters flying for about 7' without wobble. Not only was it difficult to reduce the spin rate that much but it was even more difficult to do it simultaneously with a wobble free flight. My success rate was low with so low spin rates. I was able to increase spin rate without wobble to much higher success rates. I didn't write down or memorize exact numbers but the magnitude was almost one offs to IIRC one half rotation of the putter in that 7' of flight without wobble for like 50-66% range of attempts. With slight wobble the success rate went way up with half a revolution of spin to 7'. Had i trained more for one specific version of putting the success rate of both spin rates would have likely gone up. Neither way is or has ever been my normal putting motion. So the success rates should be higher for those using one or the other of the kinds of putts all the time. I had virtually no practice for either kind of putting motion then.

Thanks for the response. Certainly the spin on the disc is relative to the initial rotational energy, and varies widely. I suppose I was really after a way to keep the disc spinning longer, as a non spinning disc seems atrociously unstable. Your work with putts would seem to back this up, not unlike other projectile stabilizing theories, like bullets. The question that launched all this for me involves disc behavior when thrown downhill. I feel like it is obvious that discs are more inclined to turn right (RHBH) when thrown downhill. This is especially impressive because sometimes the turn is quite late in the flight. What I want to know is why. Do the disc accelerate either foward or in rpm's due to gravity. It would have to be a combination I assume. I don't know that I need concrete numbers, but a simple explanation would suffice. For instance, if a disc is launched at angle X and drops Y feet, it's speed increases Z percent and it's rotation increases ?/Z percent.
KP

 

[JHern]

According to the laboratory measurements I've seen, the spin of a disc decreases approximately exponentially with time. So the spin down moment is roughly proportional to the spin rate.

Gravity is a conservative force, and does not enter into the angular momentum. Thus no effect on disc spin.

The disc moving through the air also does not seem to affect the rotation, and neither does the spin itself influence the forces and moments acting on the disc. This is why only the pitching moment is considered important (beside the spin down moment that deals with changes in spin rate) in disc flight, and is responsible for making the disc turn over or curl up depending on whether the disc is pitched up or down or up (respectively).

Scaling laws for the drag and lift coefficients are well-established: the lift involves 2 parameters and the drag involves 3 parameters. But these are 5 parameters that I do not have for any golf disc...this is why I'd love to try a wind tunnel on some discs. I'm almost ready to just get a rig and put it on my car, maybe something going high enough up and out of the sunroof...I'd still need a good force meter. But this would give me a decent estimate, even if it isn't the most accurate way to obtain such data.

The equation governing the pitching moment is not at all well constrained, and there aren't any satisfactory descriptions yet given why a disc with the same angles, spin, etc., will turn over more at higher speeds than at lower speeds and simultaneously can fade out/curl up at lower speeds. Some have proposed that it is simply a matter of angle of attack, but I'm pretty certain that it isn't so...otherwise a disc thrown nose up could never turn over, but I can indeed turn over some of my understable discs (e.g., Champion Panther), even when thrown with a lot of nose up, if I throw them at a high enough speed. So while nose up resists turn-over, the speed of the disc also matters.

I've written a flight simulator using some experimentally constrained relations I found from a Masters thesis on disc flight (from Sarah Hummel, UC Davis) and data from Potts, Crowther, and others. I put in a velocity dependence for turning vs. fading that none of the previous models had (though it is still just a simple linear dependence on velocity and angle of attack), and I'm able to get decent looking flights, i.e., they are realistic in appearance. Below is an example plot from the code, showing a nice S-line. The axes are in meters, the top plot is a side view, and the bottom plot is a map view.

Once I get some parameters into the code that I believe are representative of some standard discs, I'll begin to explore some fun questions, such as how far a disc can fly when thrown off a mountain. It is just a matter of running the code, which takes but a split second of computing time. I'd also be curious to know how it would fly if I chucked it out an airplane window, or off a high-flying hot air balloon...would it just corkscrew all the way down, or would loss of spin eventually de-stabilize it and make it fall like a tumbling object?

 

[JR]

Wouldn't one need to account for the speed range where the disc ain't flipping or fading flying flat maintaining height and not vs falling under that speed and exceeding the cruise speed. I wrote speed range on purpose because some discs seem to maintain altitude flying flat at different speeds. What i mean is that aren't parameters a continuum that may not be linear across different speeds?

 

[JHern]

Wouldn't one need to account for the speed range where the disc ain't flipping or fading flying flat maintaining height and not vs falling under that speed and exceeding the cruise speed. I wrote speed range on purpose because some discs seem to maintain altitude flying flat at different speeds. What i mean is that aren't parameters a continuum that may not be linear across different speeds?

There is no "range" of speed for which there is no turn or fade, this is a myth. There is instead a single speed where the disc doesn't turn or fade, for a given angle of attack. If it is flying one iota faster than that single speed, then it is turning over (albeit very very slowly). If it is flying one iota slower than that single speed, then it is fading (albeit very very slowly).

Things like a bead under the rim seem to make the pitching moment much less sensitive to speed around the straight-flying speed, but there is still just one speed.

And of course, it is a continuous curve. But a continuous curve can be described by a few parameters, which is the point of scaling laws and such. For example, the lift force is a linear function, with one parameter being the zero lift angle of attack, and the other being the rate of change in lift as angle of attack is varied. The drag force is a quadratic function, which has 3 parameters (min drag coeff, min drag angle of attack, and dispersion of drag as the angle of attack departs from the minimum).

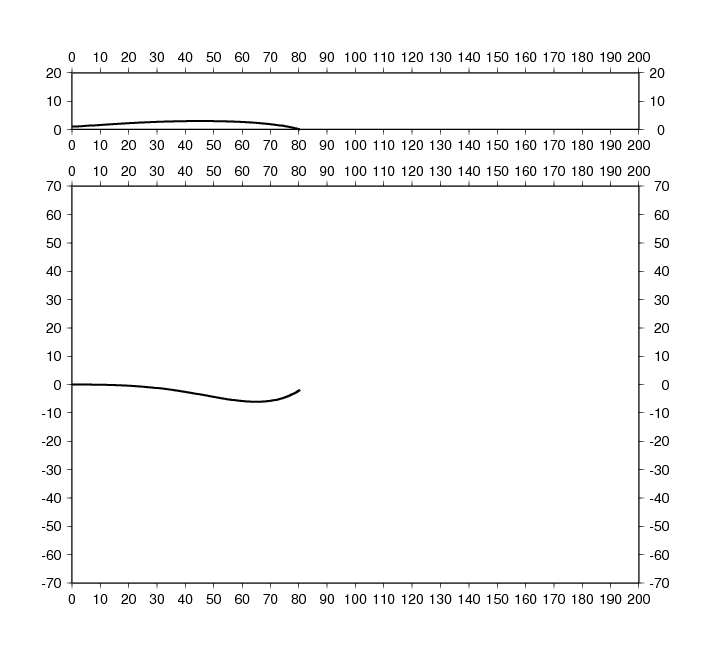
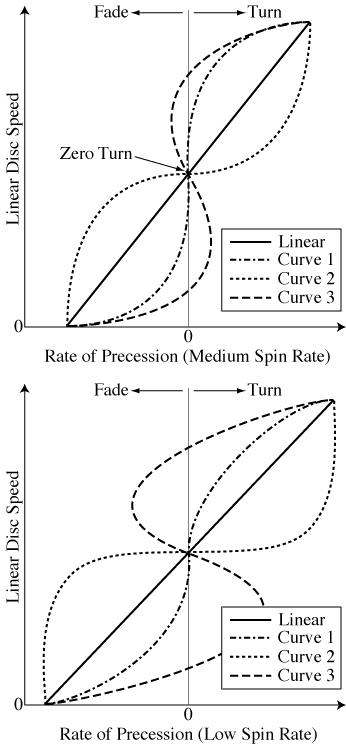
Back to the turn. Here is a figure I posted a while back...

This is the way I think we should describe discs in the future of our sport, since it covers the tendency of the disc to turn at all speeds.

I drew a number of possibilities. The top plot is for higher spin rate, the bottom is for lower spin rate. I think that a real disc is probably somewhere between "Linear" and "Curve 1." Curve 1 is what I expect for a beaded disc (think Buzzz, Stalker), following close to the zero-turn line over a range of speeds (but there is still a single speed at which it is actually zero, where the two curves intersect).

Right now I'm using a linear dependence on air speed (which goes as air speed minus zero turn speed), times a factor of total disc air speed squared so that it properly scales with the aerodynamic forces. This exact curve isn't shown on the above plot, but anyways you get the idea about how variable the behavior of a disc can be, you can draw all sorts of curves and maybe even find a disc shape that corresponds to your wildest imagination. Note that for a complete description, an additional dependence on angle of attack is needed.

Anyways, this is how it works for now in my flight simulator, although I am certain a simple linear treatment is an over-simplification. I can put whatever I want into the code, it is very simple to tweak.

But now you see why I would really like to get a better idea of the functional form for the pitching moment. This is really something extremely fundamental about the disc in flight. The rest is just basic lift and drag.

 

[Muddyboots]

Amazing. So, gravity has no effect on the rotation of the disc. Is this also true of rolling discs? Does it have no effect or is it a zero sum effect? Forgive my possibly foolish questions. On the off chance that one had access to a wind tunnel, what measurements would you be interested in?
KP

 

[JR]

Oh i should have been more precise i wasn't speaking in the terms of physics i was thinking of practical throws in real life where an inch or a half degree of movement isn't usually gonna be the deciding factor to the disc getting to birdie putt range.

As long as we are talking theoretical issues that may not be that visible in the accuracy of a throw: How about the magnus force vs gravity or should i say lift vector change with varying steepnesses of the throw? Ain't gravity pulling the disc one way, lift pushing the disc in another and magnus force possibly introducing a third force momentum going in a different direction as the other two forces possibly in another direction than the spin is going in real life applications if there is wind? And the resultant effects on turn however minute that may be. Even if it is just for one second. And that time certainly varies in practical throws from disc to disc if OAT is present. Putters won't stabilize as quickly as hog drivers. In those cases accuracy in a real throw may go down enough to be significant to scoring.

 

[jubuttib]

As long as we are talking theoretical issues that may not be that visible in the accuracy of a throw:

How about the Coriolis effect? =)

 

[JR]

I'm going to the Dutch Open so coriolis is gonna be an issue In shooting they do adjust sights when they compete abroad for coriolis.

 

[JoshEpoo]

I like the figures you've posted. I'm interested to see discs' properties described through mathematics and graphs. It's a good way to visualize how important spin and speed are.

Do you think the curves will be symmetrical like that for discs in practice? I suppose there will be inconsistencies during the inertial phase you're talking about. The most relevant part would be the portion where precession approaches 0.

Curve 3 confuses me some since we don't see discs flying like that in real life.